AlphaGeometry: новый прорыв в геометрии благодаря искусственному интеллекту. Точные и быстрые расчеты, развитие новых методов и решение сложных задач — все это доступно благодаря AlphaGeometry. Геометрия стала еще увлекательнее!
Исследователи DeepMind разработали систему искусственного интеллекта AlphaGeometry с уникальной способностью решать геометрические задачи олимпийского уровня.
Олимпиадные математические задачи представляют собой сложные математические задачи, обычно поставленные в международных математических соревнованиях, таких как Международная математическая олимпиада (ММО).
Эти задачи требуют глубокого понимания математических концепций, творческих навыков решения проблем и строгого логического мышления, охватывая такие области, как алгебра, комбинаторика и геометрия, на которые направлено данное исследование.
Исследование DeepMind, опубликованное в журнале Nature, является вехой в развитии способностей искусственного интеллекта в решении математических задач.
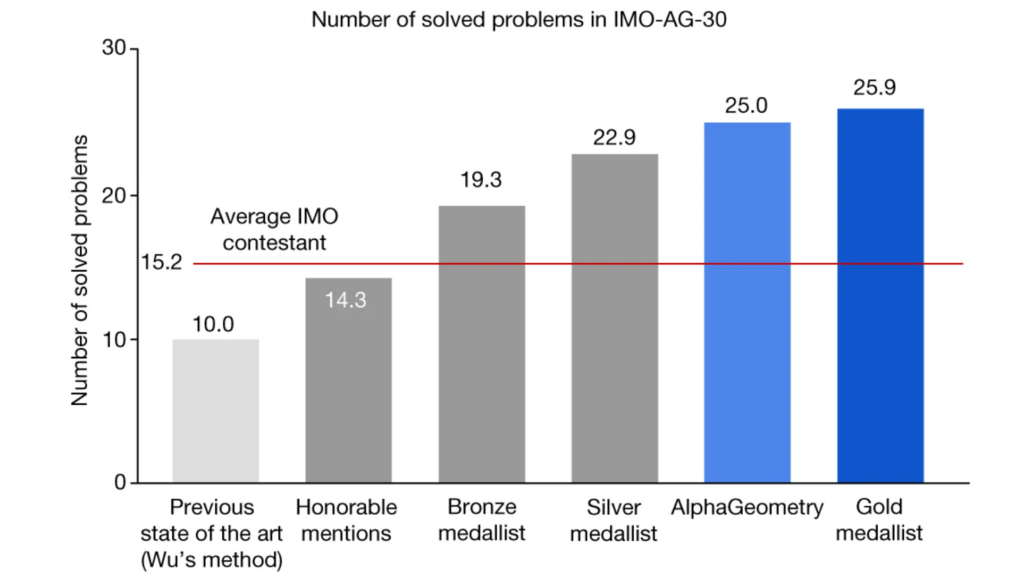
Модельная система, получившая название AlphaGeometry, успешно решила 25 из 30 задач с Международной математической олимпиады, что является значительным улучшением по сравнению с предыдущей передовой системой искусственного интеллекта, которая решила лишь 10 задач.
AlphaGeometry превзошла предыдущие модели искусственного интеллекта, но остается немного позади ведущих математиков. Источник: DeepMind через Nature.
Практически повторяя результаты человеческих обладателей золотых медалей, которые в среднем решали 25,9 задач, это впечатляющее признание навыков человеческих олимпиад. Автор исследования Три Х. Трин описывает статью ниже.
Для достижения этого искусственная система комбинирует нейронную языковую модель с символьным механизмом вывода. Нейронная модель быстро предлагает потенциальные конструкции, а символьный механизм строго выводит решения. Этот двойной подход обеспечивает баланс между скоростью и точностью в решении проблем.
Ключом к успеху AlphaGeometry стало создание 100 миллионов уникальных синтетических обучающих примеров. Этот подход позволил искусственному интеллекту обучаться без человеческого вмешательства, преодолевая основной узкий момент данных.
Примеры синтетических данных, использованных для обучения AlphaGeometry. Источник: DeepMind через Nature.
Лауреат премии Филдса и обладатель золотой медали ММО Нгу Бао Чау выразил свое удивление этим достижением, заявив в своем блоге на Google: «Теперь мне вполне понятно, почему исследователи в области искусственного интеллекта сначала пытаются решить геометрические задачи ММО, потому что поиск решений для них работает немного как шахматы в том смысле, что у нас есть довольно небольшое количество разумных ходов на каждом шаге. Но я все равно нахожу это потрясающим, что им удалось это сделать. Это впечатляющее достижение».
Эван Чен, математический тренер и бывший обладатель золотой медали олимпиады, также похвалил искусственный интеллект: «Результаты AlphaGeometry впечатляют, потому что они одновременно верифицируемы и чисты… Он использует классические геометрические правила с углами и подобными треугольниками так же, как это делают студенты».
Способность AlphaGeometry решать сложные геометрические задачи на уровне олимпиады не только демонстрирует растущую способность искусственного интеллекта логически мыслить, но также открывает новые возможности в математике и развитии искусственного интеллекта.
Если вам нужны рекомендации по управлению ИИ в бизнесе, свяжитесь с нами по адресу hello@itinai.com. Чтобы быть в курсе последних новостей об ИИ, подписывайтесь на наш Telegram-канал t.me/itinairu.
Посмотрите на практический пример решения на основе ИИ: бот для продаж от itinai.ru/aisales, созданный для автоматизации общения с клиентами круглосуточно и управления взаимодействием на всех этапах пути клиента.
Изучите, как искусственный интеллект может улучшить ваши продажи и общение с клиентами. Познакомьтесь с нашими решениями на сайте itinai.ru





















