Искусственный интеллект в математике: новые возможности и решения
Улучшение математического мышления с помощью LLMs
Искусственный интеллект значительно улучшил сложные задачи рассуждения, особенно в специализированных областях, таких как математика. Большие языковые модели (LLMs) привлекли внимание своей способностью обрабатывать большие объемы данных и решать сложные проблемы. Прогресс в математическом рассуждении этих моделей значительно улучшился благодаря новым методикам обучения, таким как Chain-of-Thought (CoT) prompting, и разнообразным наборам данных. Это позволяет моделям решать различные математические задачи, от простой арифметики до сложных задач соревнований на уровне старших классов школы.
Проблема и ее решение: мультимодальные наборы данных
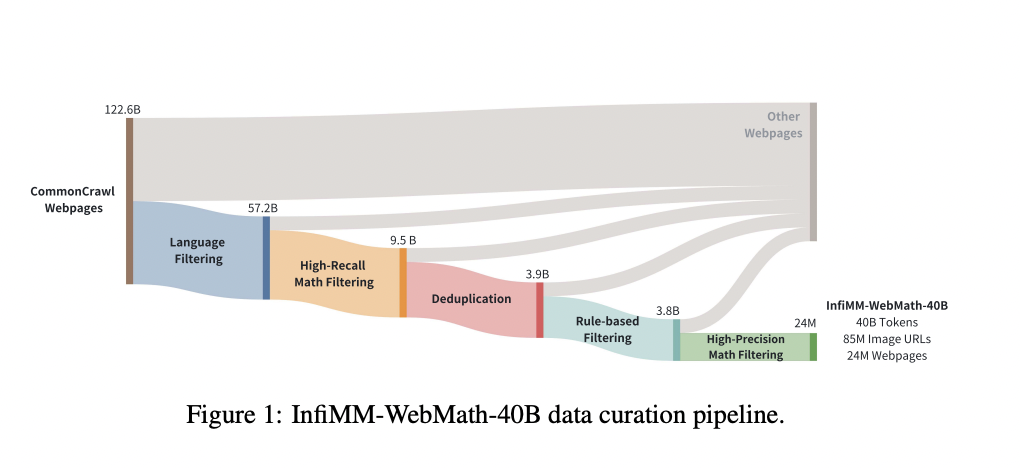
Одной из ключевых проблем, затрудняющей развитие математического рассуждения в LLMs, является отсутствие полных мультимодальных наборов данных, интегрирующих текст и визуальные данные, такие как диаграммы, уравнения и геометрические фигуры. Большинство математических знаний выражается через текстовые объяснения и визуальные элементы. В этой связи исследователи из ByteDance и Китайской академии наук представили InfiMM-WebMath-40B, обширный набор данных, предназначенный специально для математического рассуждения. Этот набор данных объединяет текстовую и визуальную математическую информацию, предоставляя уникальный ресурс для обучения мультимодальных крупных языковых моделей (MLLMs) и позволяя им обрабатывать более сложные математические концепции, чем когда-либо.
Преимущества и практическое применение
Модели, обученные на наборе данных InfiMM-WebMath-40B, показали значительное улучшение по сравнению с предыдущими наборами данных. Оценки на бенчмарках, таких как MathVerse и We-Math, подтвердили превосходство этих моделей в обработке текстовой и визуальной информации. Такие результаты подчеркивают важность интеграции визуальных элементов с текстовыми данными для улучшения математических способностей рассуждения. Набор данных InfiMM-WebMath-40B устраняет разрыв между проприетарными и открытыми моделями и открывает путь для будущих исследований по улучшению способности ИИ решать сложные математические задачи.




















