«`html
Генерализация градиентного спуска в перепараметризованных сетях ReLU: исследование стабильности минимумов и больших скоростей обучения
Градиентный спуск, обученный нейронными сетями, эффективно работает даже в перепараметризованных сетях с случайной инициализацией весов, часто находя глобальные оптимальные решения, несмотря на неконвексный характер проблемы. Эти решения, достигающие нулевой ошибки обучения, удивительно не приводят к переобучению во многих случаях, что известно как «благоприятное переобучение». Однако для сетей ReLU интерполяционные решения могут привести к переобучению. Кроме того, лучшие решения обычно не интерполируют данные в сценариях с шумными данными. Практическое обучение часто прекращается до достижения полной интерполяции, чтобы избежать попадания в нестабильные области или решений с резкими перепадами, неустойчивых.
Практические решения и ценность
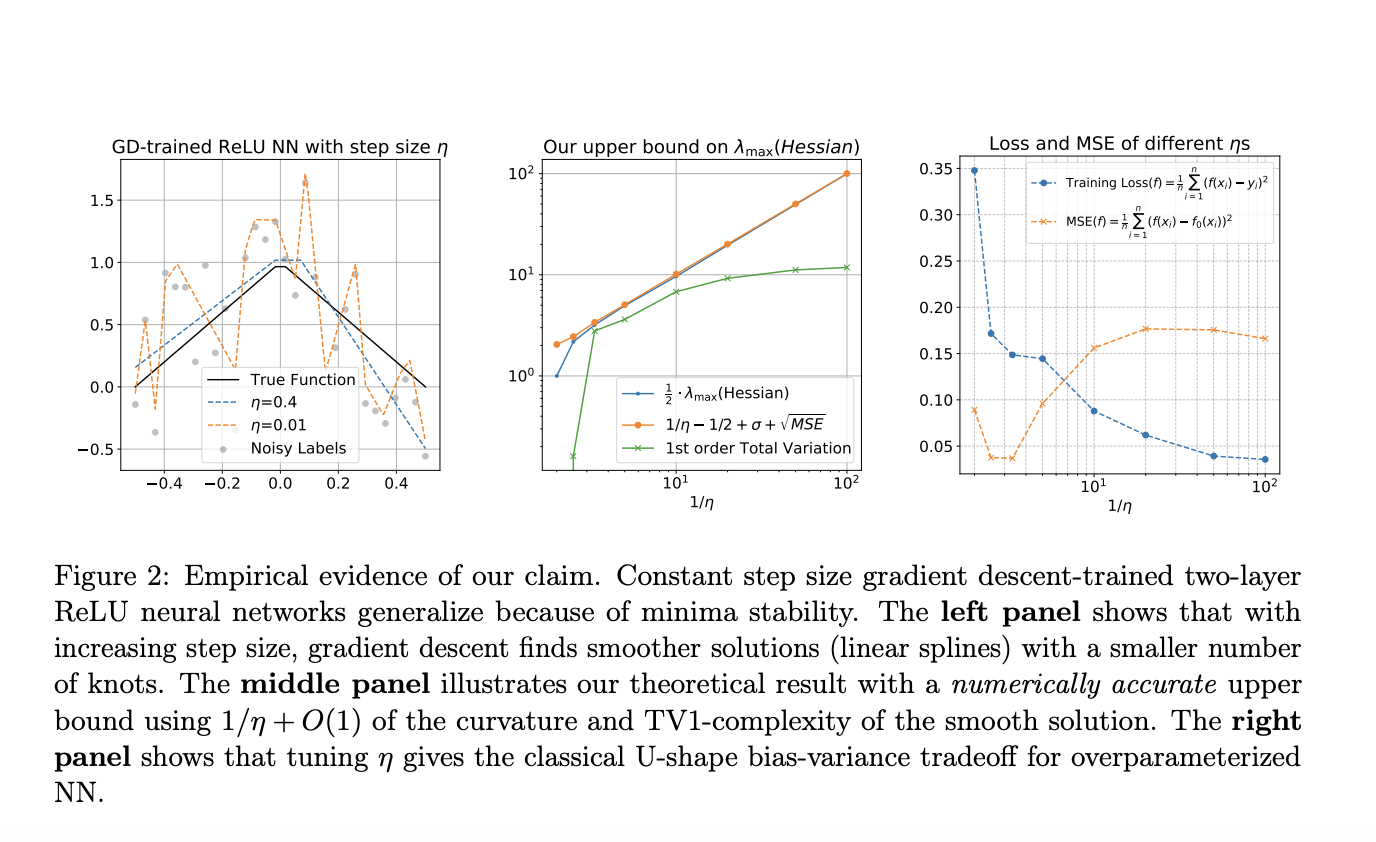
Исследователи из UC Santa Barbara, Technion и UC San Diego исследуют обобщение двухслойных нейронных сетей ReLU в 1D непараметрической регрессии с шумными метками. Они представляют новую теорию, показывающую, что градиентный спуск с фиксированным темпом обучения сходится к локальным минимумам, представляющим собой гладкие, разреженные линейные функции. Эти решения, которые не интерполируют, избегают переобучения и достигают практически оптимальных значений среднеквадратической ошибки (MSE). Их анализ подчеркивает, что большие темпы обучения вызывают неявную разреженность и что сети ReLU могут обобщаться хорошо даже без явной регуляризации или ранней остановки. Эта теория выходит за рамки традиционных ядерных и интерполяционных структур.
В перепараметризованных нейронных сетях большинство исследований сосредоточено на обобщении в пределах интерполяционного режима и благоприятного переобучения. Обычно для этого требуется явная регуляризация или ранняя остановка для работы с шумными метками. Однако недавние открытия показывают, что градиентный спуск с большим темпом обучения может достичь разреженных, гладких функций, которые хорошо обобщаются, даже без явной регуляризации. Этот метод отличается от традиционных теорий, основанных на интерполяции, демонстрируя, что градиентный спуск вызывает неявное смещение, напоминающее L1-регуляризацию. Исследование также связано с гипотезой о том, что «плоские локальные минимумы лучше обобщаются» и предоставляет понимание достижения оптимальных значений в непараметрической регрессии без затухания весов.
Исследование рассматривает настройку и обозначения для изучения обобщения в двухслойных нейронных сетях ReLU. Модель обучается с использованием градиентного спуска на наборе данных с шумными метками, с акцентом на задачи регрессии. Ключевые концепции включают стабильные локальные минимумы, которые дважды дифференцируемы и находятся на определенном расстоянии от глобального минимума. Исследование также исследует режим «Границы стабильности», где наибольшее собственное значение гессиана достигает критического значения, связанного с темпом обучения. Для непараметрической регрессии целевая функция принадлежит классу ограниченной вариации. Анализ показывает, что градиентный спуск не может найти стабильные интерполяционные решения в шумных средах, что приводит к более гладким, неинтерполирующим функциям.
Основные результаты исследования исследуют стабильные решения для градиентного спуска (GD) на нейронных сетях ReLU в трех аспектах. Во-первых, оно рассматривает неявное смещение стабильных решений в пространстве функций при больших темпах обучения, показывая, что они по своей сути более гладкие и простые. Во-вторых, оно выводит обобщающие оценки для этих решений в условиях свободного распределения и непараметрической регрессии, показывая, что они избегают переобучения. Наконец, анализ демонстрирует, что GD достигает оптимальных значений для оценки функций ограниченной вариации в определенных интервалах, подтверждая эффективную обобщающую способность решений GD с большим темпом обучения даже в шумных средах.
В заключение, исследование исследует, как обобщаются двухслойные нейронные сети ReLU, обученные градиентным спуском, через призму стабильности минимумов и явления «Границы стабильности». Оно фокусируется на одномерных входах с шумными метками и показывает, что градиентный спуск с типичным темпом обучения не может интерполировать данные. Исследование демонстрирует, что локальная гладкость функции обучения подразумевает ограничение общей вариации первого порядка на функцию нейронной сети, что приводит к исчезающему разрыву обобщения в строгом интервале поддержки данных. Кроме того, эти стабильные решения достигают практически оптимальных значений для оценки функций ограниченной вариации первого порядка при мягком предположении. Симуляции подтверждают результаты, показывая, что обучение с большим темпом обучения вызывает разреженные линейные сплайны.
Проверьте статью. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на нас в Twitter.
Присоединяйтесь к нашему Телеграм-каналу и группе LinkedIn.
Если вам нравится наша работа, вам понравится наш новостной бюллетень.
Не забудьте присоединиться к нашему 44k+ ML SubReddit.
Рады поделиться нашей последней работой, которая показывает, что «Обучение с большим шагом не может привести к переобучению» в одномерных сетях ReLU 1/
— Yu-Xiang Wang (@yuxiangw_cs) June 13, 2024
Пост Генерализация градиентного спуска в перепараметризованных сетях ReLU: исследование стабильности минимумов и больших скоростей обучения был опубликован на MarkTechPost.
Применение исследования в области искусственного интеллекта
Если вы хотите, чтобы ваша компания развивалась с помощью искусственного интеллекта (ИИ) и оставалась в числе лидеров, грамотно используйте Генерализация градиентного спуска в перепараметризованных сетях ReLU: исследование стабильности минимумов и больших скоростей обучения.
Проанализируйте, как ИИ может изменить вашу работу. Определите, где возможно применение автоматизации: найдите моменты, когда ваши клиенты могут извлечь выгоду из AI.
Определитесь какие ключевые показатели эффективности (KPI): вы хотите улучшить с помощью ИИ.
Подберите подходящее решение, сейчас очень много вариантов ИИ. Внедряйте ИИ решения постепенно: начните с малого проекта, анализируйте результаты и KPI.
На полученных данных и опыте расширяйте автоматизацию.
Если вам нужны советы по внедрению ИИ, пишите нам на https://t.me/itinai. Следите за новостями о ИИ в нашем Телеграм-канале t.me/itinainews или в Twitter @itinairu45358.
Попробуйте AI Sales Bot https://example.com/aisales. Этот AI ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж, снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab itinai.ru будущее уже здесь!
«`





















