«`html
Преодоление евклидовой парадигмы: план развития машинного обучения с геометрическими, топологическими и алгебраическими структурами
Этот документ рассматривает ограничения классических подходов машинного обучения, в первую очередь разработанных для данных, находящихся в евклидовом пространстве. Современное машинное обучение все чаще сталкивается с богато структурированными данными, которые по своей природе не являются евклидовыми, обладая сложными геометрическими, топологическими и алгебраическими структурами. Извлечение знаний из таких неевклидовых данных требует более широкой математической перспективы, выходящей за рамки традиционной евклидовой модели. Традиционные методы машинного обучения, в первую очередь разработанные для евклидова пространства, оказываются неэффективными при применении к данным с комплексными геометрическими, топологическими и алгебраическими структурами, такими как кривизна пространства-времени или нейронные связи в мозге.
Практические решения и ценность
Традиционные методы машинного обучения в основном основаны на евклидовой геометрии, где данные находятся в плоских, прямолинейных пространствах. Эти методы хорошо работают для многих обычных приложений, но испытывают трудности с неевклидовыми данными, что типично для таких областей, как нейронаука, физика и передовое компьютерное зрение. Например, евклидова геометрия не может адекватно описать изогнутые пространства общей теории относительности или сложные взаимосвязанные структуры нейронных сетей. Учитывая это ограничение, возникла область геометрического глубокого обучения, которая стремится расширить классические методы машинного обучения на неевклидовые области, используя геометрические, топологические и алгебраические структуры.
Команда исследователей из Университета Калифорнии в Санта-Барбаре, Atmo, Inc, New Theory AI, Universite C´ ote d’Azur & Inria и Университета Калифорнии в Беркли предлагает комплексную концепцию современного машинного обучения, интегрирующую неевклидовые геометрии, топологии и алгебраические структуры. Этот подход включает обобщение классических статистических и глубоких методов обучения для работы с данными, не соответствующими традиционным евклидовым предположениям. Исследователи разработали графическую таксономию, классифицирующую эти современные техники, облегчая понимание их применений и взаимосвязей. Эта таксономия уточняет существующие методы и выделяет области для будущих исследований и разработок.
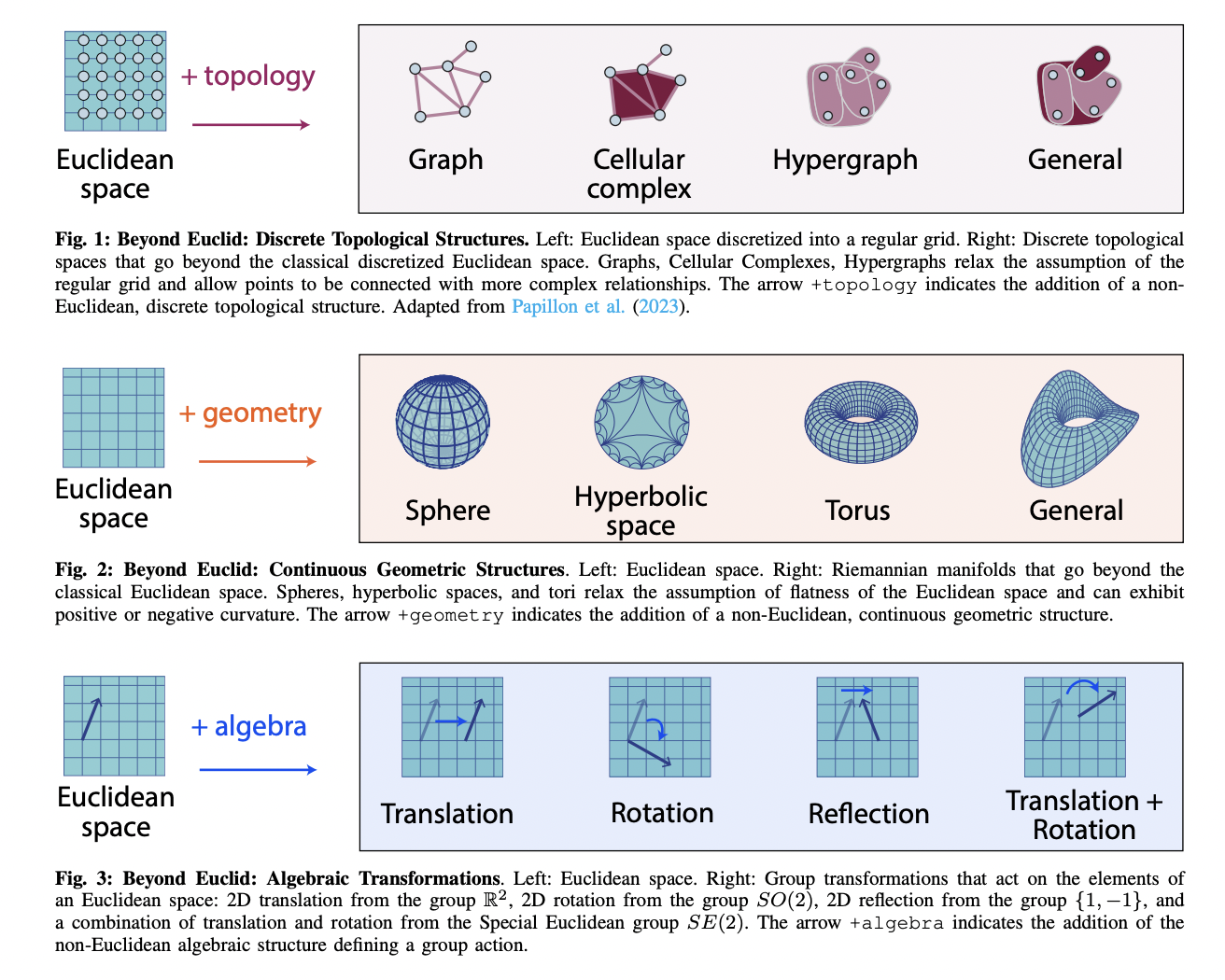
Предложенная концепция использует математические основы топологии, геометрии и алгебры для обработки неевклидовых данных. Топология изучает свойства, сохраняющиеся при непрерывных преобразованиях, такие как связность и непрерывность, которые критически важны для понимания взаимосвязей в сложных наборах данных. Например, в анализе топологических данных точки данных представлены в структурах, таких как графы или гиперграфы, которые охватывают сложные связи, выходящие за рамки возможностей евклидового пространства.
Геометрия, в частности, риманова геометрия, используется для анализа данных, находящихся на изогнутых многообразиях. Многообразия — это пространства, которые локально напоминают евклидово пространство, но могут иметь глобальную кривизну. Оборудуя эти многообразия римановой метрикой, исследователи могут определить расстояния и углы, что позволяет измерять и анализировать данные. Этот подход особенно полезен в областях, таких как компьютерное зрение, где изображения могут рассматриваться как сигналы на изогнутых поверхностях, или в нейронауке, где активность мозга отображается на сложные геометрические структуры.
Алгебра предоставляет инструменты для изучения симметрий и инвариантностей в данных с помощью действий групп. Группы, в частности, группы Ли, описывают преобразования, сохраняющие структуру данных, такие как повороты и трансляции. Эта алгебраическая перспектива необходима для задач, требующих инвариантных признаков, например, распознавание объектов в различных ориентациях. Объединяя эти математические инструменты, предложенная концепция улучшает способность моделей машинного обучения изучать и обобщать данные в неевклидовых пространствах.
Документ успешно решает ограничения традиционных методов машинного обучения в работе с неевклидовыми данными, предлагая комплексную концепцию, интегрирующую топологию, геометрию и алгебру. Этот подход расширяет область машинного обучения и открывает новые возможности для исследований и применения, что делает его значительным прорывом в этой области. Связывая классическое машинное обучение с богатыми математическими структурами, лежащими в основе реальных данных, этот подход прокладывает путь к новой эре машинного обучения, способного лучше улавливать врожденную сложность мира вокруг нас.
Проверьте документ. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на наш Twitter.
Присоединяйтесь к нашему Telegram-каналу и группе LinkedIn.
Если вам понравилась наша работа, вам понравится наша рассылка.
Не забудьте присоединиться к нашему 46k+ ML SubReddit.
Статья опубликована на портале MarkTechPost.
Применение искусственного интеллекта для вашего бизнеса
Если вы хотите, чтобы ваша компания развивалась с помощью искусственного интеллекта (ИИ) и оставалась в числе лидеров, грамотно используйте Transcending the Euclidean Paradigm: A Roadmap for Advancing Machine Learning with Geometric, Topological, and Algebraic Structures.
Проанализируйте, как ИИ может изменить вашу работу. Определите, где возможно применение автоматизации: найдите моменты, когда ваши клиенты могут извлечь выгоду из AI.
Определитесь какие ключевые показатели эффективности (KPI): вы хотите улучшить с помощью ИИ.
Подберите подходящее решение, сейчас очень много вариантов ИИ. Внедряйте ИИ решения постепенно: начните с малого проекта, анализируйте результаты и KPI.
На полученных данных и опыте расширяйте автоматизацию.
Если вам нужны советы по внедрению ИИ, пишите нам на https://t.me/itinai. Следите за новостями о ИИ в нашем Телеграм-канале t.me/itinainews или в Twitter @itinairu45358.
Попробуйте AI Sales Bot https://itinai.ru/aisales. Этот AI ассистент в продажах, помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж, снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab itinai.ru. Будущее уже здесь!
«`






















