«`html
Улучшение математического мышления в языковых моделях: интеграция метода Монте-Карло с самосовершенствованием
Современные языковые модели, такие как GPT-4 и LLaMA, благодаря быстрому развитию искусственного интеллекта значительно улучшили обработку естественного языка. Эти модели, имеющие миллиарды параметров, успешно понимают и генерируют язык, открывая новые возможности в сложных задачах, таких как решение математических проблем, системы рекомендаций и генерация молекул.
Применение в реальном мире
Однако языковые модели сталкиваются с трудностями в задачах, требующих точного рассуждения, часто допуская ошибки или «галлюцинации», особенно в математических контекстах. Несмотря на то, что методы, такие как Self-Refine, могут смягчить эту проблему, такие неточности все равно могут привести к вводящим в заблуждение или неправильным результатам в сложных прикладных задачах.
Практические решения
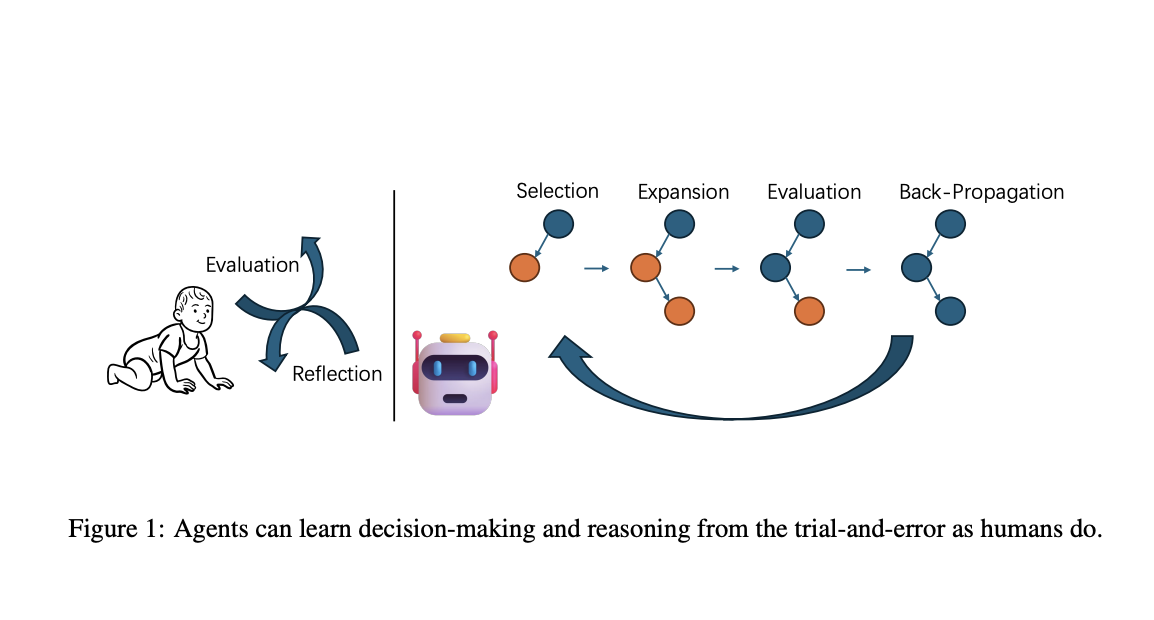
Исследователи из Университета Фудан и Шанхайской лаборатории искусственного интеллекта разработали алгоритм MCT Self-Refine (MCTSr), объединяющий языковые модели с методом Монте-Карло для улучшения математического рассуждения. Это сочетание использует систематическое исследование методом Монте-Карло и возможности самосовершенствования языковых моделей для улучшения принятия решений в сложных задачах.
Метод MCTSr позволяет значительно увеличить успешность решения математических задач на уровне олимпиад, демонстрируя потенциал для развития принятия решений и решения проблем на основе искусственного интеллекта.
Метод Монте-Карло широко применяется в различных областях для решения сложных проблем, от оптимизации многозадачного поиска пути до решения проблемы составления расписания поездов и различных задач удовлетворения ограничений (SAT). Недавние инновации включают интеграцию метода Монте-Карло с нейронными сетями, основанными на физике, для динамических задач робототехники.
Использование метода Монте-Карло в сочетании с языковыми моделями позволяет улучшить принятие решений и уточнить ответы, используя стратегическое исследование методом Монте-Карло и возможности самосовершенствования и оценки языковых моделей для повышения эффективности в сложных задачах рассуждения.
Алгоритм MCTSr значительно улучшает качество ответов в сложных задачах рассуждения, интегрируя метод Монте-Карло с большими языковыми моделями. Он итеративно улучшает ответы и оценивает их с помощью механизмов самонаграждения, обеспечивая баланс между исследованием и эксплуатацией для оптимизации принятия решений.
Для оценки эффективности алгоритма MCTSr модель LLaMA3-8B была улучшена с использованием MCTSr и протестирована на различных математических бенчмарках. Результаты показали явную корреляцию между увеличением числа итераций MCTSr и повышением успешности, особенно в более простых задачах. Однако на более сложных наборах данных производительность стабилизировалась, что указывает на ограничения текущего подхода. Сравнения с ведущими закрытыми моделями, такими как GPT-4 и Claude 3, показали, что MCTSr существенно улучшает возможности математического решения проблем открытых моделей, указывая на его потенциал для улучшения инструментов академического решения проблем.
Алгоритм MCTSr показал значительный потенциал в улучшении способности языковых моделей решать сложные математические проблемы. Путем объединения метода Монте-Карло с языковыми моделями MCTSr значительно повышает точность и надежность в математических задачах рассуждения. Экспериментальные оценки на различных наборах данных, включая сложные олимпиадные задачи, подтверждают существенные улучшения в успешности решения проблем. Хотя в настоящее время акцент сделан на математических приложениях, широкий потенциал MCTSr в областях, таких как оптимизация черного ящика и самостоятельное выравнивание для языковых моделей, указывает на перспективные направления для будущих исследований. Для полной реализации ее универсальности и эффективности требуется дальнейшее изучение и оптимизация.
Ознакомьтесь с статьей. Вся заслуга за этот исследовательский проект принадлежит его ученым. Также не забудьте подписаться на нас в Twitter.
Присоединяйтесь к нашему каналу в Telegram и группе в LinkedIn.
Если вам понравилась наша работа, вам понравится и наша рассылка.
Не забудьте присоединиться к нашему сообществу в Reddit с более чем 44 тысячами членов.
Источник: MarkTechPost.
Применение в бизнесе
Если вы хотите, чтобы ваша компания развивалась с помощью искусственного интеллекта (ИИ) и оставалась в числе лидеров, грамотно используйте Enhancing Mathematical Reasoning in LLMs: Integrating Monte Carlo Tree Search with Self-Refinement .
Проанализируйте, как ИИ может изменить вашу работу. Определите, где возможно применение автоматизацию: найдите моменты, когда ваши клиенты могут извлечь выгоду из AI.
Определитесь какие ключевые показатели эффективности (KPI): вы хотите улучшить с помощью ИИ.
Подберите подходящее решение, сейчас очень много вариантов ИИ. Внедряйте ИИ решения постепенно: начните с малого проекта, анализируйте результаты и KPI.
На полученных данных и опыте расширяйте автоматизацию.
Если вам нужны советы по внедрению ИИ, пишите нам на ITинаи. Следите за новостями о ИИ в нашем Телеграм-канале или в Twitter.
Попробуйте AI Sales Bot. Этот AI ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж и снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab. Будущее уже здесь!
«`





















