«`html
Решения в области тензорных противоречий
Тензорные противоречия используются для решения проблем, связанных с различными областями исследований, включая подсчёт модели, квантовые цепочки, графовые задачи и машинное обучение.
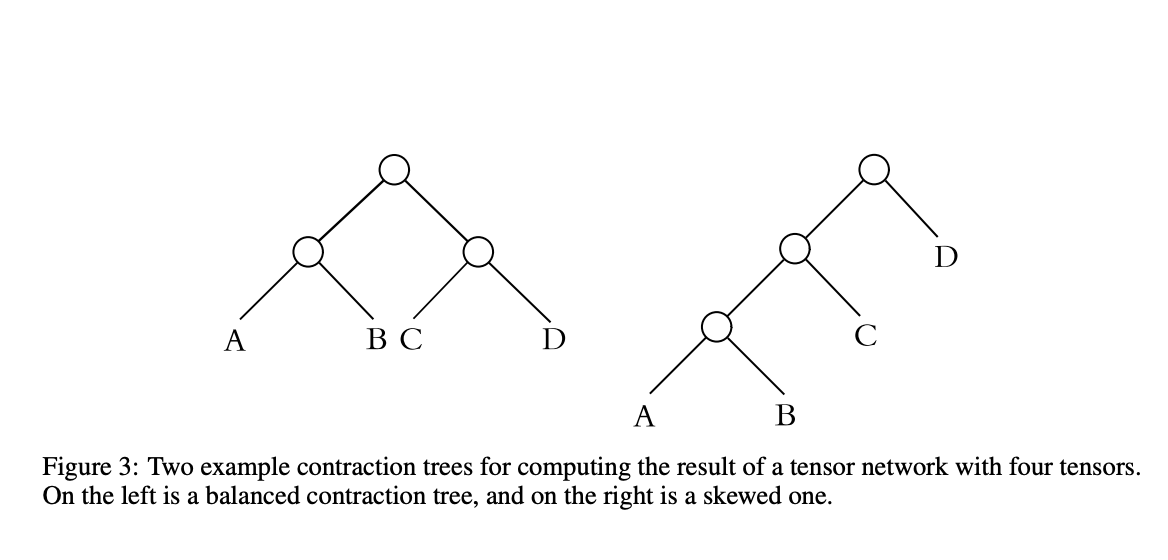
Для минимизации вычислительных затрат важно найти порядок противоречий. Результат вычислений произведения последовательности матриц A, B и C всегда будет одинаков, но вычислительные затраты будут различны в зависимости от размеров матриц.
Для улучшения времени вычислений важен выбор пути, по которому будут сокращаться тензоры друг с другом.
Применение практических решений
Ранее работы были сосредоточены на поиске эффективных путей сокращения тензорных гиперсетей. Существующие методы включают использование методов имитационного отжига, генетических алгоритмов, а также разложение графа. Команда исследователей внесла новый метод, основанный на улучшенной функции стоимости для улучшения путей сокращения тензоров.
Эксперименты и результаты
Исследователи провели два эксперимента, в которых сравнили несколько алгоритмов по нескольким критериям, таким как качество решения и вычислительное время. Новый метод показал более эффективное сокращение тензоров в меньшее время по сравнению с другими методами.
Заключение
Исследователи предложили новый подход к улучшению путей сокращения тензоров с использованием модифицированного жадного алгоритма. Новый метод показался более эффективным и быстродействующим по сравнению с другими алгоритмами.
Ссылка на оригинальную статью
Для более подробной информации ознакомьтесь с оригинальной статьей.
Свяжитесь с нами
Не стесняйтесь обращаться к нам для получения консультации или дополнительной информации о возможностях применения искусственного интеллекта в вашем бизнесе.
Slack: @itinai_ai
Telegram: itinai
Twitter: @itinairu45358
«`