«`html
Исследование Sharpness-Aware Minimization (SAM): понимание устойчивости к помехам меток и обобщения
Недавно возрос интерес к улучшению обобщения глубоких нейронных сетей путем регулирования остроты функции потерь. Метод Sharpness Aware Minimization (SAM) стал популярен благодаря своей превосходной производительности на различных бенчмарках, особенно в управлении случайными помехами меток, превосходя SGD значительно. Устойчивость SAM проявляется особенно в сценариях с помехами меток, демонстрируя существенные улучшения по сравнению с существующими техниками. Эффективность SAM сохраняется даже при недопараметризации, что потенциально увеличивает выгоды при работе с большими наборами данных. Понимание поведения SAM, особенно на ранних этапах обучения, становится ключевым для оптимизации его производительности.
Исследование механизмов SAM
Хотя механизмы SAM остаются загадкой, несколько исследований пытались прояснить значение регуляризации на примере 1-SAM. Некоторые исследователи показали, что в случае разреженной регрессии 1-SAM проявляет предвзятость к более разреженным весам по сравнению с наивным SAM. Предыдущие исследования также различают их, подчеркивая различия в регуляризации «плоскости». Недавние исследования связывают наивный SAM с обобщением, подчеркивая важность понимания поведения SAM за пределами сходимости.
Исследование устойчивости 1-SAM к помехам меток
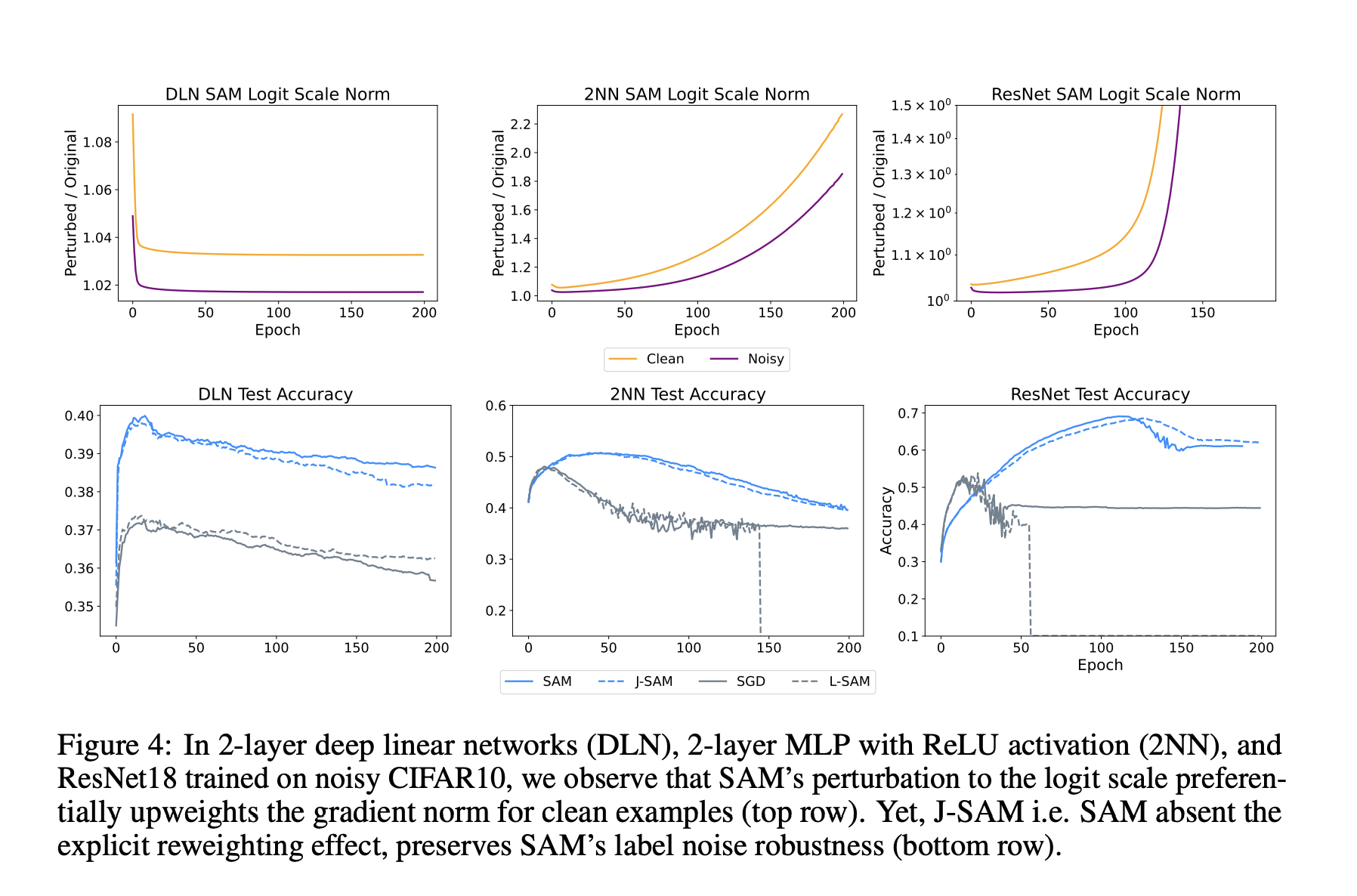
Исследователи Университета Карнеги-Меллон провели исследование, которое исследует, почему 1-SAM демонстрирует большую устойчивость к помехам меток по сравнению с SGD на механистическом уровне. Анализируя разложение градиента каждого примера, особенно сосредотачиваясь на терминах логитов и якобиана сети, исследование выявляет ключевые механизмы, улучшающие точность тестирования на ранних этапах обучения. В линейных моделях явное увеличение низких потерь точек SAM оказывается полезным, особенно в присутствии ошибочно помеченных примеров. Эмпирические результаты предполагают, что устойчивость SAM к помехам меток в основном происходит от его якобиана в глубоких сетях, указывая на фундаментально различный механизм по сравнению с термином логитов. Анализ только якобиана SAM также показывает разложение на SGD с ℓ2-регуляризацией, предлагая понимание его улучшения производительности. Эти результаты подчеркивают важность траектории оптимизации, а не свойств остроты при сходимости для достижения устойчивости SAM к помехам меток.
Экспериментальные исследования
Через экспериментальные исследования на игрушечных данных Гаусса с помехами меток SAM демонстрирует значительно более высокую точность тестирования на ранних этапах обучения по сравнению с SGD. Анализируя процесс обновления SAM, становится очевидным, что его адверсариальное возмущение весов приоритизирует увеличение сигнала градиента из точек с низкими потерями, тем самым поддерживая высокий вклад чистых примеров на ранних этапах обучения. Этот приоритет чистых данных приводит к более высокой точности тестирования до переобучения на помехи. Исследование также проясняет роль логитов в SAM, показывая, как он эффективно увеличивает градиенты из точек с низкими потерями, следовательно, улучшая общую производительность. Этот приоритет для точек с низкими потерями демонстрируется математическими доказательствами и эмпирическими наблюдениями, подчеркивая отличное поведение SAM от обновлений наивного SAM.
Практическое применение
После упрощения регуляризации SAM для включения ℓ2-регуляризации на веса последнего слоя и промежуточные активации последнего скрытого слоя в обучении глубоких сетей с использованием SGD, из-за проблем с нестабильностью пакетной нормализации исследователи заменяют ее на слой нормализации для 1-SAM. Сравнивая производительность SGD, 1-SAM, L-SAM, J-SAM и регуляризованного SGD, они обнаруживают, что, хотя регуляризованный SGD не соответствует тестовой точности SAM, разрыв значительно сужается с 17% до 9% при помехах меток. Однако в сценариях без помех регуляризованный SGD улучшается лишь незначительно, в то время как SAM сохраняет преимущество в 8% перед SGD. Это указывает на то, что, хотя не полностью объясняя преимущества обобщения SAM, аналогичная регуляризация в конечных слоях критична для производительности SAM, особенно в шумных средах.
Заключение
Это исследование направлено на предоставление устойчивой перспективы на эффективность SAM, демонстрируя его способность приоритизировать обучение на чистых примерах перед обучением на помехах, особенно в присутствии помех меток. В линейных моделях SAM явно увеличивает градиенты из точек с низкими потерями, аналогично существующим методам устойчивости к помехам меток. В нелинейных средах регуляризация промежуточных активаций и весов последнего слоя в SAM улучшает устойчивость к помехам меток, аналогично методам, регулирующим норму логитов. Несмотря на их сходства, SAM остается недостаточно изученным в области помех меток. Тем не менее, имитация аспектов регуляризации якобиана SAM может сохранить его производительность, указывая на потенциал разработки методов устойчивости к помехам меток, вдохновленных принципами SAM, несмотря на дополнительные временные затраты 1-SAM.
Проверьте статью. Вся заслуга за это исследование принадлежит исследователям этого проекта. Также не забудьте подписаться на наш Twitter. Присоединяйтесь к нашему каналу в Telegram, Discord и группе в LinkedIn.
Если вам понравилась наша работа, вам понравится наша рассылка.
Не забудьте присоединиться к нашему сообществу в Reddit с более чем 41 тысячей участников.
Не забудьте присоединиться к нашему сообществу в Телеграм-канале и Twitter.
Попробуйте AI Sales Bot itinai.ru/aisales. Этот AI ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж и снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab itinai.ru — будущее уже здесь!
«`




















