«`html
Колмогоров-Арнольдовские сети (KAN) как альтернатива традиционным MLP
Колмогоров-Арнольдовские сети (KAN) представляют собой перспективную альтернативу традиционным многослойным перцептронам (MLP). Они используют нейроны, выполняющие простые операции сложения. Однако текущая реализация KAN представляет определенные вызовы в практических приложениях. Исследователи в настоящее время рассматривают возможность идентификации альтернативных многомерных функций для KAN-нейронов, которые могли бы предложить улучшенную практическую ценность в нескольких бенчмарках, связанных с задачами машинного обучения.
Возможное применение KAN и их улучшение
Исследования выявили потенциал KAN в различных областях, таких как компьютерное зрение, анализ временных рядов и поиск квантовой архитектуры. Некоторые исследования показывают, что KAN могут превзойти MLP в задачах подгонки данных и уравнений в частных производных, используя меньшее количество параметров. Однако некоторые исследования вызвали опасения относительно устойчивости KAN к шуму и их производительности по сравнению с MLP. Также рассматриваются вариации и улучшения стандартной архитектуры KAN, такие как графовые модели, сверточные KAN и трансформерные KAN для решения возникающих проблем. Кроме того, исследуются альтернативные функции активации, такие как вейвлеты, радиальные базисные функции и синусоидальные функции для улучшения эффективности KAN. Несмотря на эти работы, существует потребность в дальнейших улучшениях для повышения производительности KAN.
Новый подход к улучшению KAN
Исследователь из Центра исследования прикладных интеллектуальных систем Университета Халмстад, Швеция, предложил новый подход для улучшения производительности Kolmogorov-Arnold Networks (KAN). Этот метод направлен на определение оптимальной многомерной функции для KAN-нейронов в различных задачах классификации машинного обучения. Традиционное использование сложения в качестве функции на уровне узла часто неидеально, особенно для высокомерных наборов данных с несколькими признаками. Это может приводить к тому, что входы превышают эффективный диапазон последующих функций активации, что приводит к нестабильности обучения и снижению обобщающей производительности. Для решения этой проблемы исследователь предлагает использовать среднее вместо суммы в качестве функции узла.
Эксперименты и результаты
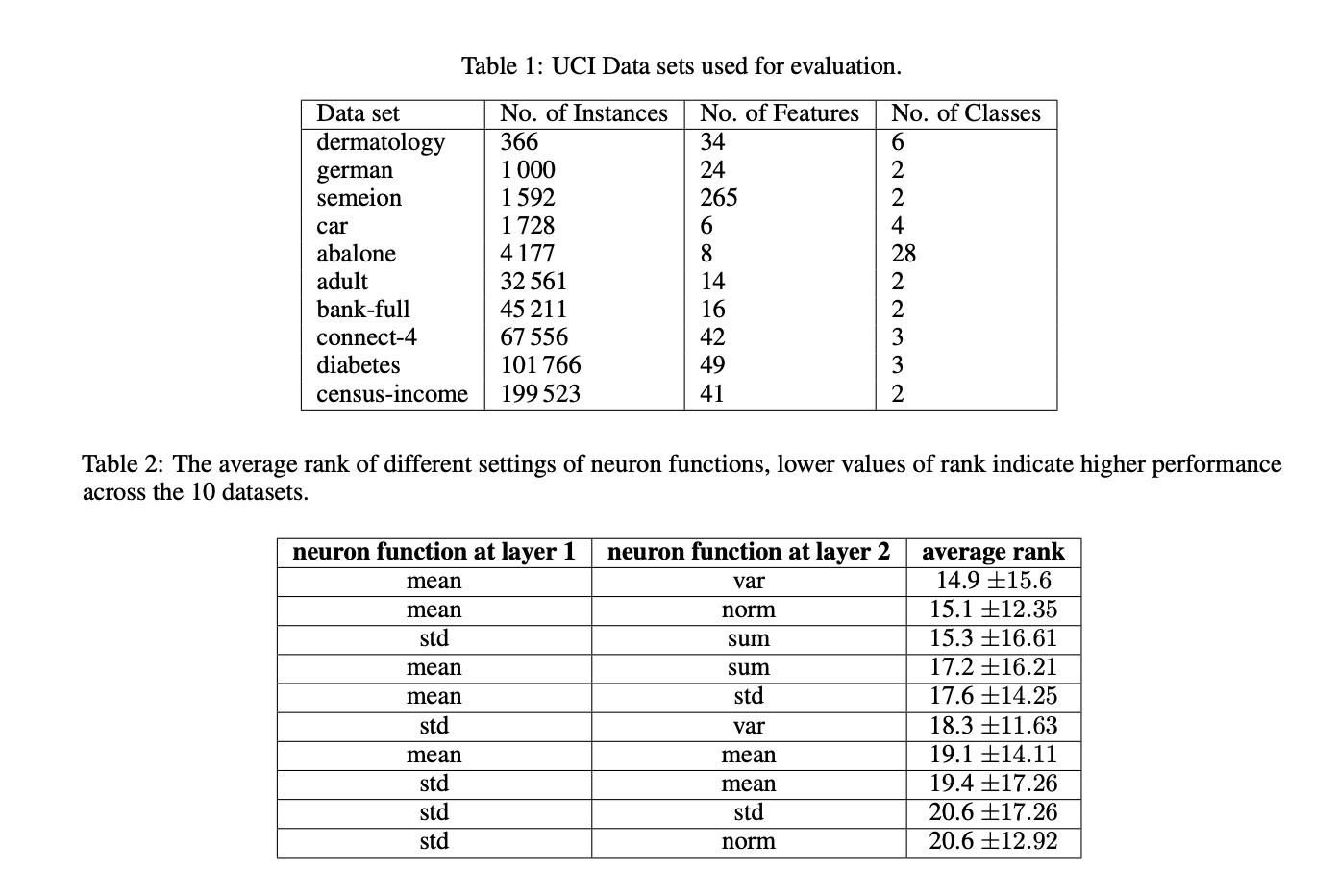
Для оценки предложенных модификаций KAN использовались 10 популярных наборов данных из репозитория баз данных машинного обучения UCI. Результаты подтверждают гипотезу о том, что использование средней функции в нейронах KAN эффективнее, чем традиционная сумма. Это улучшение обусловлено способностью среднего значения сохранять входные значения в оптимальном диапазоне сплайновой функции активации, который составляет [-1.0, +1.0]. Стандартные KAN испытывали трудности с сохранением значений в этом диапазоне в промежуточных слоях при увеличении количества признаков. Однако использование средней функции в нейронах приводит к улучшению производительности, сохраняя значения в требуемом диапазоне для наборов данных с 20 или более признаками.
Применение в бизнесе
Если вы хотите, чтобы ваша компания развивалась с помощью искусственного интеллекта (ИИ) и оставалась в числе лидеров, грамотно используйте The Kolmogorov-Arnold Theorem Revisited: Why Averaging Functions Work Better. Проанализируйте, как ИИ может изменить вашу работу, определите, где возможно применение автоматизации, определитесь с ключевыми показателями эффективности (KPI) для улучшения с помощью ИИ. Подберите подходящее решение, внедряйте ИИ решения постепенно, на полученных данных и опыте расширяйте автоматизацию.
AI Sales Bot и другие продукты
Попробуйте AI Sales Bot https://itinai.ru/aisales. Этот AI ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж и снижать нагрузку на первую линию. Узнайте, как ИИ может изменить ваши процессы с решениями от AI Lab itinai.ru. Будущее уже здесь!
Подробнее описанные исследования доступны в статье «The Kolmogorov-Arnold Theorem Revisited: Why Averaging Functions Work Better».
«`