«`html
Улучшение стабильности в моделировании: универсальный подход с использованием тестирования на основе центральной предельной теоремы
Методика стабилизации моделирования
Метод дистилляции модели представляет собой способ создания интерпретируемых моделей машинного обучения путем использования более простой «учащейся» модели для репликации прогнозов сложной «учительской» модели. Однако, если производительность учащейся модели существенно различается при различных обучающих наборах данных, ее объяснения должны быть более надежными. Существующие методы стабилизации дистилляции включают в себя создание достаточного количества псевдоданных, но они часто адаптированы под конкретные типы учащихся моделей. Стратегии, такие как оценка стабильности критериев принятия решений в деревьях и отбор признаков в линейных моделях, используются для решения этой проблемы. Эти подходы, хотя и полезные, ограничены зависимостью от конкретной структуры учащейся модели.
Исследователи из Университета Калифорнии в Беркли и Университета Пенсильвании предлагают универсальный метод стабилизации дистилляции модели с использованием подхода центральной предельной теоремы. Их рамочная методика начинается с использования нескольких кандидатов учащихся моделей для оценки того, насколько хорошо они соответствуют учительской модели. Они применяют множество тестовых структур для определения необходимого размера выборки для последовательных результатов на различных псевдовыборках. Этот метод демонстрируется на деревьях решений, списке опускающихся правил и моделях символьной регрессии с применением на наборах данных молочных желез и рака груди. Исследование также включает теоретический анализ с использованием процесса Маркова и чувствительного анализа на факторы, такие как сложность модели и размер выборки.
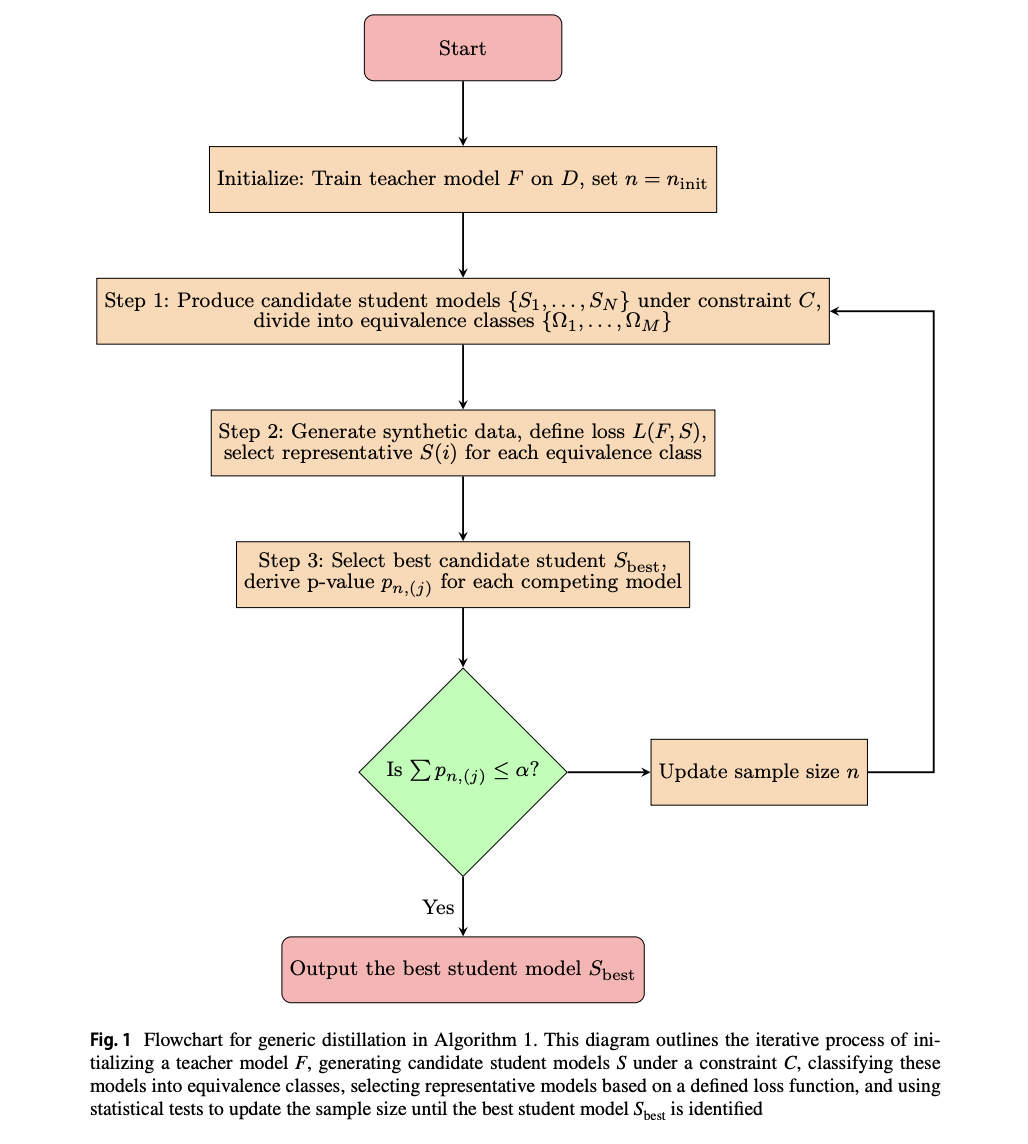
Исследование представляет стабильный подход к моделированию с использованием асимптотических свойств среднего убытка на основе центральной предельной теоремы. Эта рамочная методика используется для определения вероятности выбора фиксированной структуры модели на основе различных псевдовыборок и расчета необходимого размера выборки для контроля этой вероятности. Кроме того, исследователи реализуют множество тестовых процедур для учета конкурирующих моделей и обеспечения стабильности выбора модели. Метод включает в себя создание синтетических данных, выбор лучшей учащейся модели из кандидатских структур и итеративное корректирование размеров выборки до выявления значимой модели.
Исследователи специально затрагивают три понятные учащиеся модели — деревья принятия решений, списки опускающихся правил и символьную регрессию — демонстрируя их применимость для предоставления интерпретируемых и стабильных объяснений модели. С использованием статистических симуляций Монте-Карло, байесовского отбора и генетического программирования, мы создаем разнообразные кандидатские модели и классифицируем их в эквивалентные классы на основе их структуры. Этот подход контрастирует с ансамблевыми методами за счет фокуса на стабильности и воспроизводимости в выборе модели, обеспечивая последовательные объяснения для учительской модели на различных выборках данных.
Эксперименты на двух наборах данных с использованием универсального алгоритма дистилляции модели, с фокусом на чувствительный анализ ключевых факторов. В настройках включается бинарная классификация с потерями перекрестной энтропии, фиксированная модель случайного леса и генерация синтетических данных. Эксперименты включают 100 запусков с различными зернами. Гиперпараметры включают уровень значимости (альфа) 0,05, начальный размер выборки 1000 и максимальную длину 100 000. Метрики оценки охватывают стабильность интерпретации и достоверность учащейся модели. Результаты показывают, что стабилизация улучшает последовательность структуры модели, особенно в отборе признаков. Чувствительный анализ показывает, что увеличение кандидатских моделей и размера выборки улучшает стабильность, в то время как сложные модели требуют больших выборок.
Исследование представляет стабильный метод дистилляции модели с использованием проверки гипотез и тестовой статистики на базе центральной предельной теоремы. Подход гарантирует создание достаточного количества псевдоданных для выбора последовательной структуры учащейся модели из кандидатов. Теоретический анализ представляет проблему в виде процесса Маркова, предоставляя границы сложности стабилизации с комплексными моделями. Эмпирические результаты подтверждают эффективность метода и указывают на сложность отличия сложных моделей без обширных псевдоданных. Будущая работа включает уточнение теоретического анализа с использованием границ Берри-Эссена и классов Донскера, рассмотрение неопределенности учительской модели и изучение альтернативных процедур множественного тестирования.
Проверьте статью и репозиторий на GitHub. Вся заслуга за это исследование принадлежит ученым, проводившим это исследование. Также не забудьте подписаться на нас в Twitter и вступить в наш Telegram-канал и группу LinkedIn. Если вам понравилась наша работа, вам понравится и наша рассылка.
Не забудьте присоединиться к нашему сообществу в ML SubReddit.
Найдите предстоящие вебинары по ИИ здесь.
Используйте ваше представление о возможностях ИИ, чтобы продвинуть вашу компанию вперед. Сделайте шаг к использованию автоматизации: определите, где в вашем бизнесе можно применить ИИ. Выберите подходящее решение из множества вариантов ИИ. Внедряйте ИИ постепенно: начните с маленького проекта, оцените результаты и КПЭ.
На основе полученного опыта расширяйте автоматизацию.
Если вам нужна помощь во внедрении ИИ, свяжитесь с нами на https://t.me/itinai. Следите за новостями о ИИ в нашем телеграм-канале t.me/itinainews или в Twitter @itinairu45358.
Ознакомьтесь с AI Sales Bot здесь. Этот AI ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж и снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с помощью решений от AI Lab itinai.ru, будущее уже здесь!
«`





















